다룰 정렬 알고리즘
간단하고 느린 알고리즘
- bubble_sort
- insertion_sort
- selction_sort
빠른 알고리즘
- quick_sort
- merge_sort
- heap_sort
O(N)
- radix_sort
simple & slow
Selection Sort 선택정렬
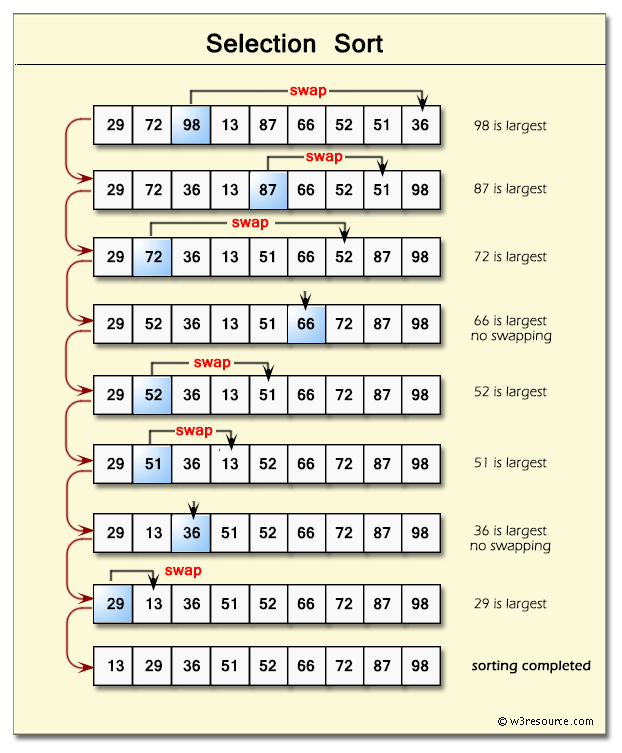
- 배열의 맨 마지막 값(배열[length-1]과 배열[0] 부터 배열[length-2]값 사이의 최대값을 swap하고,
- 최대값은 배열의 맨 마지막 값(배열[length-1]이 된다.
- 동일한 동작을 배열의 맨 마지막 값을 빼고 재진행하여 배열의 크기가 1이 될 때까지 반복한다.
Psuedo code
1
2
3
4
5
6
selectionSort(A[], n) { //배열 A[1...n]을 정렬한다.
for (last가 n-2까지 감소) {
A[1...last] 중 가장 큰 수 A[k]를 찾는다
A[k]와 A[last]값을 교환
}
}
실행시간
- for문 : 루프가 n-1번 반복
- A[1…last] 중 최대값 찾기 : n-1번, 다음 루프에서는 n-2번, …, 2번, 1번으로 줄어듦
- 예) 3개 값 중 최대값을 찾으려면 2번 비교, 4값 중 최대값을 찾으려면 3번 비교해야됨
- swap : 상수시간 작업
시간복잡도
T(n) = (n-1) + (n-2) + (n-3) + … + 2 + 1 = n(n-1)/2 = O(n^2)
Bubble sort 버블 정렬
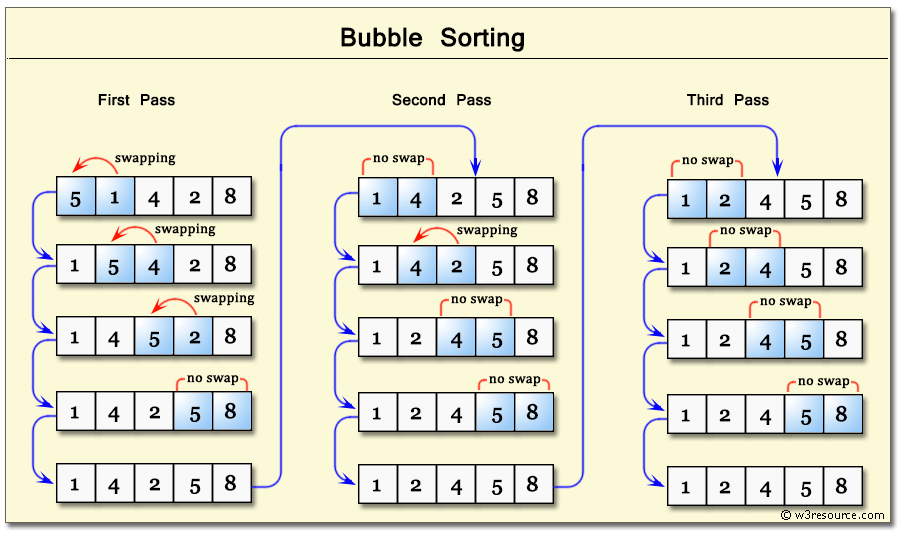
- 배열의 최대값을 구해 배열의 맨 끝값과 swap한다는 방식은 선택정렬과 유사하나,
- 최대값을 맨 끝으로 가져오는 방식이 조금 다르다.
- 배열의 첫 번째 값과 두 번째 값을 비교하여 최소값을 배열[0]으로 swap한다.
- 해당 동작을 배열[0]을 제외한 배열에서 반복하여 배열의 크기가 1이 될 때까지 반복하면 배열[0]은 최소값, 배열[length-1]은 최대값이 된다.
Psuedo code
1
2
3
4
5
6
7
8
9
10
bubbleSort(A[], n) { //배열 A[1...n]을 정렬한다.
for (last가 n-2까지 감소) {
for (i = 0; i < last-1; i++) { //반복문에서
if (A[i] > A[i+1]) {
// 더 작은 값을 앞으로 보낸다
A[i]와 A[i+1]을 교환
}
}
}
}
실행시간
- for문 : 루프가 n-1번 반복
- 2개의 값 비교 : n-1번, 다음 루프에서는 n-2번, …, 2번, 1번으로 줄어듦
- swap : 상수시간 작업
시간복잡도
T(n) = (n-1) + (n-2) + (n-3) + … + 2 + 1 = n(n-1)/2 = O(n^2)
Insertion Sort 삽입 정렬
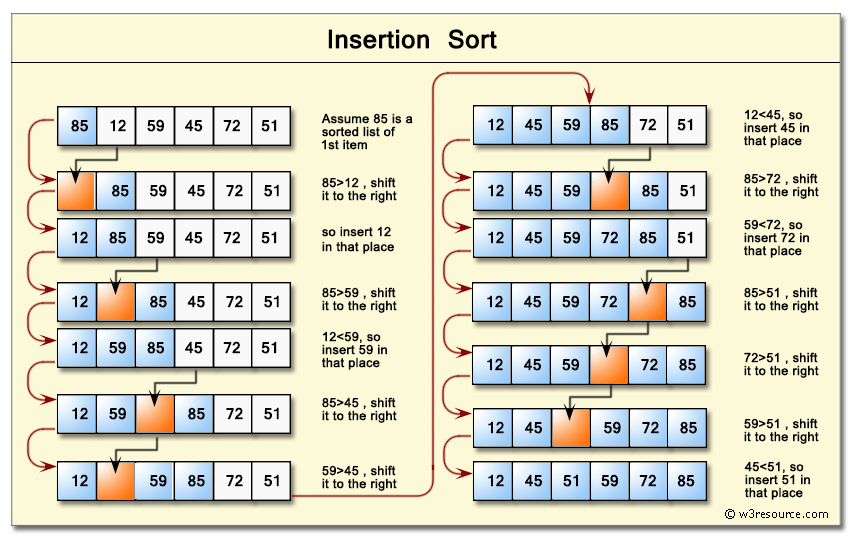
- 배열의 초기값에는 값이 1개, 즉 배열[0]만 있다고 가정하고,
- 배열에 추가할 값을 배열[0]과 비교해서 배열[0]보다 작으면 배열[0]은 배열[1]이 되고, 배열[0] 자리에 추가할 값을 넣는다.
- 다시 배열에 추가할 값과 길이가 2가 된 배열을 비교하여 배열[0], 배열[1], 배열[2] 중 어디에 들어가야할지 비교하여 인덱스가 정해진다.
- 해당 자리에 추가할 값을 삽입한다.
- 위 동작을 배열의 크기가 다 채워질 때까지 반복한다.
Psuedo code
1
2
3
4
5
6
insertionSort(A[], n) { //배열 A[1...n]을 정렬한다.
for (i = 1; i < last-1; i++) {
//반복문에서
A[0~i]의 적당한 자리에 A[i]를 삽입
}
}
실행시간
- for문 : 루프가 n-1번 반복
- 삽입은 최악의 경우 i-1번 반복
시간복잡도
T(n) = (n-1) + (n-2) + (n-3) + … + 2 + 1 = n(n-1)/2 = O(n^2)
- 최악의 경우 버블정렬, 선택정렬과 동일한 시간복잡도를 갖지만,
- 만일 원본 배열이 정렬이 되어있는 상태라면 n-1로 끝나기 때문에,
- 평균적으로는 버블정렬과 선택정렬의 절반 정도의 시간만 필요